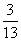 ,3周完成这项工程的( ),还剩下这项工程的( )。
,3周完成这项工程的( ),还剩下这项工程的( )。
答:
;
查看答案
答:
140÷=840(米)
查看答案
下列两小题只列算式(或方程),不用计算。
①一项工程,甲单独做6天完成,乙单独做9天完成。两人合做这项工程,多少天可以完成?
②食堂买来一些大米,3天吃了其中的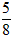 ,还剩下150千克。求这些大米共有多少千克?
,还剩下150千克。求这些大米共有多少千克?
①一项工程,甲单独做6天完成,乙单独做9天完成。两人合做这项工程,多少天可以完成?
②食堂买来一些大米,3天吃了其中的
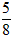 ,还剩下150千克。求这些大米共有多少千克?
,还剩下150千克。求这些大米共有多少千克?
答:
①1÷;②150÷
查看答案
答:
“略”
查看答案
答:
甲、乙交替工作所需整周期:1÷(+)≈5(个)甲、乙各干5小时后还剩的工作量:1-(+)×5=剩下的公作量由甲做需要:÷=(小时)完成这项工程共需的时间:5×2+=10(小时)
查看答案
答:
略,具体答案请查看详情
查看答案
答:
(天)
查看答案
答:
略,具体答案请查看详情
查看答案
答:
解:设甲的工作效率为a,则乙为a,丙为a。3×(8a+12×a)÷(9×a)=12(天)
查看答案
答:
略,具体答案请查看详情
查看答案
答:
解:设原有x台机器,规定的时间为y小时,则有:xy=(x+2)y解得x=1414y=(14-2)(y+),解得y=414×4=56(小时)
查看答案
答:
解:由题可知,甲乙合作需要天,乙丙合作需要天,丙甲合作需要天,三队合作一天能完成总工作量的:(++)×2=,则甲乙丙的工作效率分别为为:甲:﹣=,(甲4天完成);乙:﹣=,(乙5天完成);丙:﹣=,(8天完成,排除)甲乙合作一天需要的费用为:1800×=810(元)乙丙合作一天需要的费用为:1520×=494(元)甲丙合作一天需要的费用为:1680×=630(元)则甲乙丙合作一天需要的费用为:(810+494+630)×2=967(元)则甲、乙、
查看答案
答:
8﹣3=5(天),(﹣×3)÷5=,1÷(﹣)=20(天)。
查看答案
答:
(1﹣)÷(1÷20+1÷30)=÷(+)=÷=×=(天);所以两队合作了天完成这项工程。
查看答案
答:
甲的工作效率:1÷8=,乙的工作效率:1÷12=,工作效率的和:+=,合做工程的一半需要的天数:÷=2(天)
查看答案
答:
解:1÷(+)=1÷,=12(天);答:两队合作需要12天完成。
查看答案
答:
将甲、乙各干1小时看做1个周期,则完成总工程量需:合作7个周期还剩的工作量:剩下的工作由甲完成需:完成这项工程共需:
查看答案
答:
原计划的工作时间:1÷(+)=12(天),现在的工作时间:12+2=14(天),甲的工作量:×(14﹣2)=×11.5=;乙实际干的时间:(1﹣)÷=×30=12(天);乙休息的时间:14﹣12=1(天),答:乙休息了1天。
查看答案
答:
解:1÷(+)=(天)
查看答案
答:
解:(1-×15)÷(+)=3(天)答:甲乙两队合作了3天。
查看答案
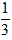 ,第二周修了140米,两周正好修了一半,这条路长多少米?
,第二周修了140米,两周正好修了一半,这条路长多少米?
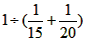 求的是__________。
求的是__________。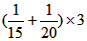 求的是__________。
求的是__________。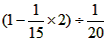 求的是__________。
求的是__________。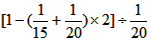 求的是__________。
求的是__________。
 小时完成,乙单独做
小时完成,乙单独做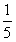 小时完成,甲、乙合做需要( )小时完成。
小时完成,甲、乙合做需要( )小时完成。
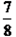 就可以完成,如果减少2台机器,那么就要推迟
就可以完成,如果减少2台机器,那么就要推迟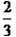 小时做完。问:由一台机器完成这项工程需要多少时间?
小时做完。问:由一台机器完成这项工程需要多少时间?
 天可以完成,需支付1800元;由乙丙两队承包3又
天可以完成,需支付1800元;由乙丙两队承包3又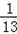 天可以完成,需支付1520元;由丙甲两队承包2又
天可以完成,需支付1520元;由丙甲两队承包2又 天可以完成,需支付1680元.在保证7天内完成的条件下,选择哪个队单独承包的费用最少?这个最少的费用是多少元?
天可以完成,需支付1680元.在保证7天内完成的条件下,选择哪个队单独承包的费用最少?这个最少的费用是多少元?
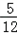 ,如果这条路由乙队单独修,那么乙队多少天可以修完这条路?
,如果这条路由乙队单独修,那么乙队多少天可以修完这条路?
 后,乙队又加入施工,两队合作了多少天完成这项工程?
后,乙队又加入施工,两队合作了多少天完成这项工程?
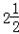 天,乙休息了若干天,这样比预计之日推迟了2天完工,问乙休息了多少天?
天,乙休息了若干天,这样比预计之日推迟了2天完工,问乙休息了多少天?
