分数的四则混合运算及应用题大全及答案
更新时间:2021-06-23
类型:小学六年级数学题
题数:1414
答:
8﹣3=5(天),(﹣×3)÷5=,1÷(﹣)=20(天)。
查看答案
答:
(+)×4=×4=;(1﹣)÷==(小时);所以还要小时完成。
查看答案
答:
22.4;4.5;7;69;90.8;8
查看答案
答:
(1)7.15+110÷(3.2×2.3)=7.15+110÷7=7.15+14=22 (2)=5.6×[10÷(6.1﹣6)]=5.6×[10÷0.1]=5.6×100=560 (3)=÷[(﹣)×]=÷[×]=÷11=(4)1+2﹣3﹣4+5+6﹣7﹣8+9+…+1993=(1+2﹣3﹣4)+(5+6﹣7﹣8)+9+&h
查看答案
答:
(1)篮球个数;(2)排球个数;(3)排球个数;(4)篮球个数
查看答案
答:
520÷(1﹣)=520÷(1﹣)=520÷=2400(元)答:这台电视机2400元。
查看答案
答:
解:设上学期男生有x人,则女生有750﹣x人,根据题意可得方程:(1+)x+(1﹣)×(750﹣x)=710,x+600﹣x=710, x=110, x=300,则本学期的男生有(1+)×300=350(人),则女生有710﹣350=360(人),答:本学期男生有350人,女生有360人。
查看答案
答:
(3.625)=﹣3.625﹣4.375=9﹣(3.625+4.375)=9﹣8=1
查看答案
答:
第二根绳子对应的分率:1+=,第一根绳子长:210÷(1+)=210÷=78.75(米);答:第一根绳子长78.85米。
查看答案
答:
解:设做丙元件x个,则需做甲元件5x个,做乙元件3x个,做丙元件需安做丙元件需安排x人,做甲元件需安排x人,做乙元件需安排x人,x+x+x=41,x=41, x÷=41÷, x=24,做丙元件需安排:×24=8(人),做甲人元件需安排:×24=15(人),做乙元件需安排:×24=18(人),答:安排做甲、乙、丙三种元件各15人、18人、8人,才能使生产的三种元件正好配套。
查看答案
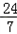 小时
小时