答:
(1)因为共有10张奖卷,一个一等奖,所以抽得一等奖的概率为:1÷10=110;(2)因为共有10张奖卷,两个二等奖,小明抽中一个二等奖,所以还剩9张奖卷,一个二等奖,所以他再次抽中二等奖的概率为:1÷9=19;故答案为:110,19.
查看答案
答:
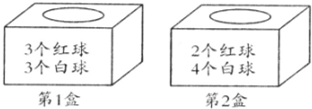
3÷(3+3),=3÷6,=12;0÷(2+4)=0,从第1盒中任意摸出一个球.摸出白球的可能性是12.从第2盒中任意摸出一个球,摸出黑球的可能性是0;故答案为:12,0.
查看答案
答:
(1)(2)因为中一等奖的可能性占是18,获得二等奖的可能性为14,获得三等奖的可能性为12,抽到“谢谢光顾”的可能性是18,有中一等奖的可能,只是可能性比较小;
查看答案
答:
一粒有1~6共六个数字的骰子,随便怎么投掷,出现数字“7”的可能性为0;故答案为:0.
查看答案
答:
可能;一定;不可能;一定;不可能
查看答案
答:
6÷34-6,=8-6,=2(个);6-2=4(个);故答案为:4.
查看答案
答:
(1)1÷5=15;(2)2÷5=25;(3)4÷5=45;答:摸到5的可能性是15,摸到偶数的可能性是25,摸到小于5的可能性是45;故答案为:15,25,45.
查看答案
答:
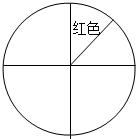
14×12=18;答:指针停在红色区域的可能性是18.故答案为:18.
查看答案
答:
事件发生的可能性:p=发生可能的情况数出现情况的总数×100%;故答案为:发生可能情况数,出现情况的总数.
查看答案
答:
见下图:
查看答案
答:
(1)4÷(54-2),=4÷52,=113;(2)1÷(54-2),=1÷52,=152;(3)13÷(54-2),=13÷52,=14;答:抽到5的可能性是113,抽到红心5的可能性是152,抽到黑桃的可能性是14;故答案为:113,152,14.
查看答案
答:
由分析知,(1)1÷2=12;答:正面朝上的可能性是12.(2)抛硬币只能会出现正面朝上和反面朝上两种结果,每种结果朝上的可能性都为12,但是抛每次硬币都是一个独立事件,下一次的结果不会受前一次的影响,每种结果朝上的可能性都会发生,所以“小萱试验了20次,只有6次正面朝上.”的这种结果是有可能发生的,(3)虽然第一次是正面朝上,但第二次又是一个独立事件,与前面的没有关联,所以不能确定第二次是正面还是反面朝上;因为硬币只有正反两面,抛出去的硬币落地时可能正面向上,也可能
查看答案
答:
脑筋急转弯占14=28,趣味数学占38,谜语竞猜占28,英语歌曲占1-14-38-14=18,设计转盘如下,黄色区域表示脑筋急转弯,黑色区域表示趣味数学,红色表示谜语竞猜,绿色区域表示英语歌曲.
查看答案
答:
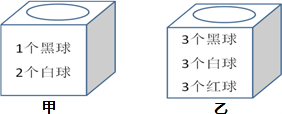
(1)2+1=3(个),黑球:1÷3=13;白球:2÷3=23;(2)3×3=9(个),白球:3÷9=13,23>13,所以,从甲箱里摸到白球的可能性大一些;答:从甲箱里摸到黑球的可能性是13,从甲箱里摸到白球的可能性大一些.故答案为:13,甲.
查看答案
答:
①6×16=1(个)6×13=2(个)②6×16=1(个)③6×56=5(个)故答案为:1,2,1,5.
查看答案
答:
黑色区域的份数是:10×15=2,白色区域的份数是:10×12=5,灰色区域的份数是:10×310=3;如下图:100×15=20(次);答:如果转动转盘100次,那么大约有20次指针指在黑色区域.
查看答案
答:
12×23=8(部分);
查看答案
答:
2÷(1+2+3)=2÷6=13故选:b.
查看答案
答:
因为12+13+16=1,假设共放6个球,应放:紫球:6×12=3(个),白球:6×132(个),红球:6×16=1(个);答:放入6个球,紫球应放3个,白球应放2个,红球应放1个.
查看答案
答:
(1)红铅笔:15×13=5(枝),蓝铅笔:10-5=10(枝);答:放5枝红铅笔,10枝蓝铅笔.(2)红铅笔:18×23=12(枝),蓝铅笔:18-12=6(枝);答:放12枝红铅笔,6枝蓝铅笔;(3)摸到红铅笔的可能性是14,红铅笔放1枝,蓝铅放3枝.故答案为:5,10,12,6,1,3.
查看答案