新洋小学有368名同学是1995年出生的，其中六年级（3）班里38名学生。

他们说得对吗？为什么？  

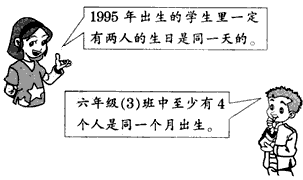
答： 对。因为1995年共365天，把它看做是365个抽屉，把368名同学放入365个抽屉，至少有一个抽屉里有2名同学，因此其中一定有两个人的生日在同一天的。一年有12个月，把它看成12个抽屉，把38名同学放入12个抽屉，至少有一个抽屉里有4名同学，因此至少有4名学生是同一个月出生的。 查看答案

查看答案

幼儿园大班有26个小朋友，至少有（    ）个小朋友是同一个月出生的。 

答： 3 查看答案

查看答案

把6根黄瓜放到4个盘子里，至少有（    ）根黄瓜放进同一个盘子里。

答： 2 查看答案

查看答案

有7个不相同的自然数，其中至少有两个数的差是6的倍数，这是为什么？

答： 一个自然数除以6的余数，只能是0、1、2、3、4、5。如果有两个自然数除以6的余数相同，那么这两个自然数的差就是6的倍数，一个自然数除以6的除数，可能是0、1、2、3、4、5。所以把这6种情况看做6个抽屉，把任意7个不同的自然数，看做7个元素，根据抽屉原理，必有一个抽屉中至少有两个数，而这两个数的余数是相同的，它们的差一定是6的倍数。 查看答案

查看答案

把7个蘑菇放在2个篮子里，至少有（    ）个蘑菇放在同一个篮子里。

答： 4 查看答案

查看答案

一个布袋里有白、黑、红三种颜色的钥匙链各8个（同一大小同一样式），每次从布袋里拿出一个，最少要拿出多少个才能保证其中至少有2个颜色不同的钥匙链？

答： 9个 查看答案

查看答案

一些孩子在海洋馆里玩海洋球。

答： 我们把6堆海洋球看做任意6个自然数，它们被5除，其余数不外乎是0、1、2、3、4五种可能，如果把每一种余数看做一个抽屉，那么余数相同的两数就在同一个抽屉里，根据抽屉原理，6个自然数除以5后，必有两个数的余数相同，显然必有两数之差是5的倍数。 查看答案

查看答案

把165本书分给五年级（3）班的学生，如果其中至少有1人分到5本日记本。那么，这个班最多有多少人？

答： 41人 查看答案

查看答案

一个幼儿园大班有50名小朋友。班里有各种玩具155件，把这些玩具分给小朋友。是否有人会得到4件或4件以上的玩具？

答： 会 查看答案

查看答案

把4个苹果放入3个果盘，一共可以有（    ）种摆放方法。（把下面的统计表填写完整）

摆放方法

第一种

第二种

第三种

第四种

……

第一盘

0

0

第二盘

0

1

第三盘

4

3

 

答： 4；0；2；2；1；1；2 查看答案

查看答案

夏令营活动共有2000名儿童参加。他们可以参加登陆小岛、参观海底世界和参观森林植物园三个项目。如果规定每人必须参加两个项目，那么至少有多少名儿童参加的项目完全相同？

答： 667 查看答案

查看答案

盒子里有同样大小的红球和黄球各15个，至少拿出（    ）个，才能保证拿出来2个同色球。

答： 3 查看答案

查看答案

5块糖果要分给4个小朋友，总有一个小朋友至少分到（    ）块糖果。

答： 2 查看答案

查看答案

盒子里有同样大小的红球和黄球各10个，至少拿出（    ）个，才能保证拿出来2个红色球。

答： 12 查看答案

查看答案

五年级有3个班，在一次数学竞赛中，至少要有几人获奖？才能保证一定有4名同学是同班的。

[     ]

a．8        
b．9    
c．10

答： c 查看答案

查看答案

在围棋子中，至少取出（    ）棋子，就可以保证有相同颜色的棋子。

答： 3个 查看答案

查看答案

把红、黄、白、蓝四种颜色的球各5个放到一个口袋里，至少取出（    ）球，可以保证取到白颜色的球。

答： 16个 查看答案

查看答案

在13个人里，至少有2个人出生在同一年。

[     ]

答： 错误 查看答案

查看答案

把7个核桃分给3个同学，至少有一名同学得到4个核桃。    

[     ]

答： 错误 查看答案

查看答案

7名学生，至少2人六年级。

[     ]

答： 错误 查看答案

查看答案