| 在一张三角形纸内任作2009个互不重合的点(所有的点都不在三角形的任意一条边上),以这2009个点和三角形纸的3个顶点为顶点的三角形,最多能剪出多少个? |
| 根据题干分析可得: 三角形内的每个点最多能够提供360°的圆周角,那么把图形完全剪开后,所有小三角形的内角和加起来不能超过360°×2009+180°,所以小三角形的个数不能超过 (360°×2009+180°)÷180°=4019(个) 答:最多能剪4019个三角形. |
关注公众号回复:奥数答案
即可免费获得密码查看答案

[ ]
a.缩小为原来的[ ]
[ ]
a.4.5÷l.5 ,那么积
,那么积[ ]
a.扩大为原来的5倍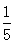
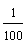 ,另一个因数不变,积
,另一个因数不变,积[ ]
a.扩大为原来的100倍
奥数库(www.aoshuku.com)是一个专注奥数知识扩展和学习的在线教育网站,内容涵盖了奥数题、数学题、试卷、课件、知识点、数学公式等,拥有大量的奥数题库和数学题库,包含全国中小学各个版本教材,深受中小学师生用户喜爱的网站。
奥数库专注奥数知识分享,如有版权作品存在问题或内容中存在违法和不良信息,请立即联系403074932@qq.com