| 有125个同样大小的正方体木块,木块的每个面的面积均为1平方厘米,其中63个表面涂上白色,还有62个表面涂上蓝色.将这125个正方体木块粘在一起,形成一个棱长为5厘米大正方体木块.这个大正方体木块的表面上,蓝色的面积最多是______平方厘米. |
| 据题可知,大正方体显然是5×5×5(cm)拼凑方法; 由大正方体结构可知,一个小木块位于大正方体的顶点时,它有三个面处表大正方体表面; 当小木块位于大正方体的棱的位置时,它有两个面处于表面,其余位置则至多只有一个面可以处于表面; 所以要将蓝色小正方体尽可能多的位于顶点和棱的位置上,蓝色小木块占据大正方体8个顶点时, 处于表面的蓝色表面积为:总面积为1×8×3=24(cm2); 蓝色小木块完全占据大正方体12条棱除去顶点之外的位置时,处于表面的蓝色表面积为:1×36×2=72(cm2); 则剩余的蓝色小木块个数是:62-8-36=18(个),使它们都有一个面能够算在大正方体表面积上,面积为:18×1=18(cm2); 所以,总的蓝色面积最多为24+72+18=114(cm2). 故答案为:114cm2. |
关注公众号回复:奥数答案
即可免费获得密码查看答案

 要用( )个正方体。搭23个这样的图形,需要多少个正方体?
要用( )个正方体。搭23个这样的图形,需要多少个正方体?
 要用3个小正方体。摆13个这样的图形要用多少个小正方体?
要用3个小正方体。摆13个这样的图形要用多少个小正方体?
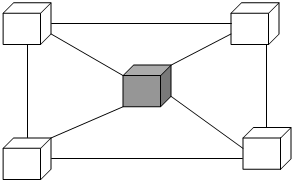
 这种图形,可以搭几个?
这种图形,可以搭几个?

奥数库(www.aoshuku.com)是一个专注奥数知识扩展和学习的在线教育网站,内容涵盖了奥数题、数学题、试卷、课件、知识点、数学公式等,拥有大量的奥数题库和数学题库,包含全国中小学各个版本教材,深受中小学师生用户喜爱的网站。
奥数库专注奥数知识分享,如有版权作品存在问题或内容中存在违法和不良信息,请立即联系403074932@qq.com