一串数排成一行,它们的规律是这样的:头两个数都是1,从第三个数开始,每一个数都是前两个数的和,也就是:1,1,2,3,5,8,13,21,34,55,… 问:这串数的前100个数中(包括第100个数)有多少个偶数?
观察一下已经写出的数就会发现,每隔两个奇数就有一个偶数,如果再算几个数,会发现这个规律仍然成立.这个规律是不难解释的:因为两个奇数的和是偶 数,所以两个奇数后面一定是偶数.另一方面,一个奇数和一个偶数的和是奇数,所以偶数后面一个是奇数,再后面一个还是奇数.这样,一个偶数后面一定有连续 两个奇数,而这两个奇数后面一定又是偶数,等等.因此,偶数出现在第三、第六、第九……第九十九个位子上.所以偶数的个数等于100以内3的倍数的个数, 它等于99÷3=33
关注公众号回复:奥数答案
即可免费获得密码查看答案



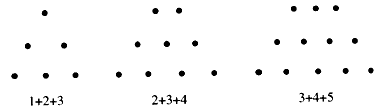
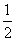 =
=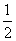 -
-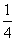 =
=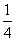 -
-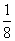 =根据上面的规律计算:1-
=根据上面的规律计算:1-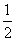 -
-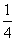 -
-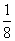 -
-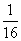 -
-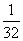 -
-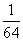 -
-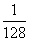
奥数库(www.aoshuku.com)是一个专注奥数知识扩展和学习的在线教育网站,内容涵盖了奥数题、数学题、试卷、课件、知识点、数学公式等,拥有大量的奥数题库和数学题库,包含全国中小学各个版本教材,深受中小学师生用户喜爱的网站。
奥数库专注奥数知识分享,如有版权作品存在问题或内容中存在违法和不良信息,请立即联系403074932@qq.com