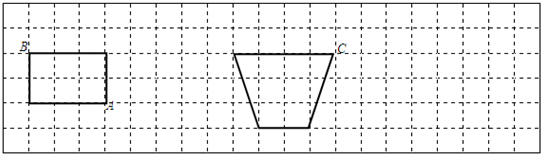
| 如图,abcd是一个梯形,e是ad的中点,直线ce把梯形分成甲、乙两部分,它们的面积之比是10:7。求ab与cd的长度比。 |
|
|
设△ace和△ecd的高为h,△acb和△acd的高为h1。
s△ace= ×ae×h,s△dce=
×ae×h,s△dce=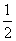 ×ae×h
×ae×h
e中ad的中点,s△ace=s△dce
s四边形abce:s△aed=10:7,s四边形abce=s△abc+s△ace
s△abc:s△adc=3:14
s△abc=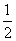 ×ab×h1,s△adc=
×ab×h1,s△adc=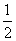 × cd×h1
× cd×h1
ab:cd=3:14
关注公众号回复:奥数答案
即可免费获得密码查看答案



[ ]
a.平行四边形面积[ ]
a.面积[ ]
a.面积奥数库(www.aoshuku.com)是一个专注奥数知识扩展和学习的在线教育网站,内容涵盖了奥数题、数学题、试卷、课件、知识点、数学公式等,拥有大量的奥数题库和数学题库,包含全国中小学各个版本教材,深受中小学师生用户喜爱的网站。
奥数库专注奥数知识分享,如有版权作品存在问题或内容中存在违法和不良信息,请立即联系403074932@qq.com