A、B 是一圈形道路的一条直径的两个端点,现有甲、乙两人分别从 、 两点同时沿相反方向绕道匀速跑步(甲、乙两人的速度未必相同),假设当乙跑完100米时,甲、乙两人第一次相遇,当甲差60米跑完一圈时,甲、乙两人第二 次相遇,那么当甲、乙两人第十二次相遇时,甲跑完几圈又几米?
甲、乙第一次相遇时共跑圈,乙跑了100米;第二次相遇时,甲、乙共跑1.5圈,则乙跑了100×3=300米,此时甲差60米跑一圈,则可得0.5圈是300-60=240米,所以一圈是480米.第一次相遇时甲跑了240-100=140米,以后每次相遇甲又多跑140×2=280米,所以第十二次相遇时甲共跑了140+280×11=3220:米,即跑了6圈340米.
关注公众号回复:奥数答案
即可免费获得密码查看答案

[ ]
a.30千米[ ]
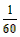 。
。 [ ]

奥数库(www.aoshuku.com)是一个专注奥数知识扩展和学习的在线教育网站,内容涵盖了奥数题、数学题、试卷、课件、知识点、数学公式等,拥有大量的奥数题库和数学题库,包含全国中小学各个版本教材,深受中小学师生用户喜爱的网站。
奥数库专注奥数知识分享,如有版权作品存在问题或内容中存在违法和不良信息,请立即联系403074932@qq.com