答:
12 540 75 262.5
查看答案
答:
4.7
查看答案
答:
略,具体答案请查看详情
查看答案
答:
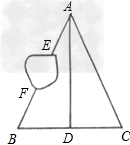
解:由题意,知bd=cd,∠bda=∠cda=90°,ad=ad,则△adb≌△adc,所以ab=ac=3,故斜拉桥至少有3﹣1.2﹣0.7=1.1(千米)。
查看答案
答:
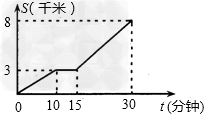
解:(1)3千米;修车用了15﹣10=5(分钟);(2)30分钟;(3)小亮修车前的速度为(千米/分钟),按此速度到校共需时间为(分钟),(分钟),则他比实际情况早到学校3.3分钟。
查看答案
答:
解:设a、b两地相距x千米,则可得:,解得:x=90经检验:x=90是原方程的解,并且符合题意所以可得原计划小时到达,答:两地相距90千米;原计划9.5小时到达。
查看答案
答:
-50+10=-40(米);答:鲨鱼所在的高度是-40米.
查看答案
答:
(-5-4+0+3+6+8)÷6+80,=8÷6+80,≈1.3+80,=81.3(米);答:这几个月的实际水位是81.3米.
查看答案
答:
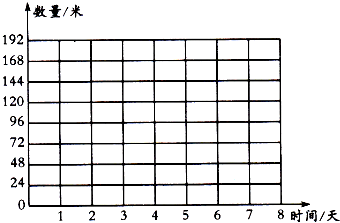
(1)时间/天123456…数量/米24487296120144…(2)(3)成正比例因为铺设总长度÷天数=24米(一定)(4)24×8=192(米)100÷24≈4(天)答:8天能铺设192米管道,铺设100米管道大约需要4天.
查看答案
答:
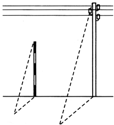
(1)3:2=4.5:3=6:4=7.5:5=9:6=1.5;杆高:影长=1.5(一定);杆高和影长的比值一定,那么杆高和影长成正比例;(2)设电线杆高x米,由比例关系可得:1.8:1.2=x:3.2,1.2x=1.8×3.2,1.2x=5.76,1.2x÷1.2=5.76÷1.2,x=4.8;答:电线杆高4.8米.故答案为:杆高影长=1.5;杆高,影长,正.
查看答案
答:
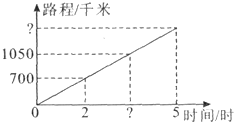
如图,(1)700÷2=350(千米/时),1050÷350=3(小时),答:这列列车要行驶1050千米需要3小时.(2)350×5=1750(千米),答:这列列车5小时可以行驶1750千米.
查看答案
答:
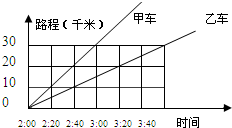
(1)2080÷3060=12;(2)15÷12=30(分钟);或15×3060÷2080=30(分钟);答:乙车速度是甲车速度的12,甲车15分钟行的路程,乙车需要30分钟.
查看答案
答:
解:800×4.5-3400=200(米)
查看答案
答:
解:(726-69× l)÷4.5- 69=77(千米/时)
查看答案
答:
解:(1)(17.6 - 8.00)÷1.6+3=9(千米) (2) 若选择往返坐车,需付费: 8.00+(6×2-3)×l.2 =8+9×l.2 =18.8(元) 若选择单程坐车,共需付费: 8.00×2+(6-3)×l.6×2 =16+9.6 =25.6(元)故坐往返车比较合算。
查看答案
答:
解:两人没相遇:(100+120)×12.5+150=2750+150=2900(米) 两人相遇:(100+120)×12.5-150=2600(米)
查看答案
答:
解:(1)4+(8-3)×1.6=12(元) (2)(20 - 4)÷1.6+3=13(千米)
查看答案
答:
900÷4.5-110=90(千米)
查看答案
答:
80-60÷2=50(米/分)292.5÷(80-50)=9.75(分)9.75×80=780(米)
查看答案
答:
(56+60)×4.5
查看答案