答:
①根据分数单位的意义,158的分数单位是18.②2-138=38,所以再加上3个这样的分数单位就是最小的质数.故答案为:18,3.
查看答案
答:
(1)145的分母是5,所以分数单位是15;(2)最小的质数是2,2-145=15,即再加上1个这样的分数单位后是最小的质数.故答案为:15,1.
查看答案
答:
根据真分数的意义可知,分数单位是17的最大真分数是67;2-67=87,所以它最少要添上8个这样的分数单位就是最小的质数.故答案为:67,8.
查看答案
答:
(1)11小的分母是小,所以分数单位是1小,分子是11,所以它有11个这样的分数单位;(小)最小的质数是小,11小-小=p小,即减去p个这样的分数单位后是最小的质数.故答案为:1小,11,p.
查看答案
答:
(1)分数单位是19的最大真分数是89;(2)最小的质数是2,2-89=109,即再加10个这样的单位就是最小的质数.故答案为:89,10.
查看答案
答:
这个数是210001004,读作:二亿一千万一千零四;故答案为:210001004,二亿一千万一千零四.
查看答案
答:
(1)这个数是:219000;(2)219000≈22万;故答案为:219000,22万.
查看答案
答:
(1)根据数位顺序表,写出这个数为:240001000;数级亿级万级个级数位…千亿位百亿位十亿位亿位千万位百万位十万位万位千位百位十位个位…240001000(2)240001000=24000.1万,240001000≈2亿;故答案为:200041000,20004.1万,2亿.
查看答案
答:
这个数是:5070701;5070701=507.0701万.故答案为:5070701,507.0701万.
查看答案
答:
;23
查看答案
答:
;7;9
查看答案
答:
这样的自然数有4个:23,37,53,73
查看答案
答:
四个瓶子与油的总重量为:(8+9+10+11+12+13)÷3=63÷3=21(千克)符合条件的质数是2(4个瓶的重量)和19(4瓶油的重量)(注:19千克不可能是瓶重,否则2瓶就超过8千克了)故最重的两瓶油重:13-2÷4×2=13-1=12(千克)答:最重的两瓶内共有油12千克。
查看答案
答:
先将a+b+c化为3(a+2b)的形式,说明a+b+c是3的倍数,然后利用整除的性质对a、b被3整除后的余数加以讨论得出a+2b也为3的倍数.∵ =a+b+2a+5b=3(a+2b),显然,3│a+b+c若设a、b被3整除后的余数分别为ra、rb,则ra≠0, rb ≠0.若ra≠rb,则ra=2,rb=1或ra=1,rb=2,则2a+5b =2(3m+2)+5(3n+1)=3(2m+5n+3),或者2a+5b=2(3p+1)+5(3q+2);3(2P+59+4),即2a+5b为合数与已
查看答案
答:
解答: 首先确定能保证平均分的范围,再根据质数的要求,确定具体的数值。17被3除余2,被4除余1,要满足题目的条件,根据余数的加法原理,每堆块数都必须是被3除余2,被4除余1的质数。所以只需要找出被3除余2,被4除余1的100以内的余数即可,首先容易找到满足条件最小的质数为5,因为3和4的最小公倍数是12,只需要依次加上12,然后核对是不是质数就能全部找出来,那么可以得出100以内这样的质数有:5、17、29、41、53、89这六个,它们的和是234,所以桌上放的糖块最多是234块。
查看答案
答:
分析:根据题意,设出两个质数,再根据题中的数量关系,列出方程,再根据未知数的取值受限,解答即可.解答:解:设a,b是满足题意的质数,根据一个两位质数写在另一个两位质数后面,得到一个四位数,它能被这两个质数之和的一半整除,那么有100a+b=k(a+b)÷2( k为大于0的整数),即(200-k)a=(k-2)b,由于a,b均为质数,所以k-2可以整除a,200-k可以整除b,那么设k-2=ma,200-k=mb,( m为整数),得到m(a+b)=198,由于a+b可以被2整除,所以m是99的
查看答案
答:
两位的质数有11,13,17,19,23,29,3l,37,41,43,47,53,59,6l,67,71,73,79,83,89,97.可得出,最小为11+19=13+17=30,最大为97+71=89+79=168.所以满足条件的a+b最小可能值为30,最大可能值为168.
查看答案
答:
因为是质数所以个位数不可能为偶数0,2,4,6,8也不可能是奇数5.如果末位数字是3或9,那么数字和就将是3或9的两倍,因而能被它们整除,这就不是质数了.所以个位数只能是7.这个三位质数可以是167,257,347,527或617中间的任一个.
查看答案
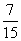 的分数单位是( ),再添上( )个这样的分数单位就等于最小的质数。
的分数单位是( ),再添上( )个这样的分数单位就等于最小的质数。
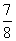 的分数单位是( ),它含有( )个这样的分数单位,增加( )个这样的分数单位是最小的质数。
的分数单位是( ),它含有( )个这样的分数单位,增加( )个这样的分数单位是最小的质数。
