题目与解析

答案与解析

先将a+b+c化为3(a+2b)的形式，说明a+b+c是3的倍数，然后利用整除的性质对a、b被3整除后的余数加以讨论得出a+2b也为3的倍数．

∵ =a+b+2a+5b=3(a+2b)，

显然，3│a+b+c

若设a、b被3整除后的余数分别为ra、rb，则ra≠0， rb ≠0．

若ra≠rb，则ra=2，rb=1或ra=1，rb=2，则2a+5b =2(3m+2)+5(3n+1)=3(2m+5n+3)，或者2a+5b=2(3p+1)+5(3q+2)；3(2P+59+4)，即2a+5b为合数与已知c为质数矛盾．

∴ 只有ra=rb，则ra=rb=1或ra=rb=2．

于是a+2b必是3的倍数，从而a+b+c是9的倍数．

又2a+5b=2×11十5×5=47时，=

a+b+c=11+5+47=63，

2a+5b =2×13十5×7=61时，

a+b+c =13+7+61=81，

而(63，81)=9，故9为最大可能值．

【小结】由余数切入进行讨论，是解决整除问题的重要方法．

关注公众号回复：奥数答案

即可免费获得密码查看答案

密码错误

查看答案

微信搜索天才奥数关注公众号

手机扫码关注公众号

查看答案

查看答案

密码错误

热题推荐

• 万尼亚想了一个三位质数，各位数字都不相同.如果个位数字等于前两个数字的和，那么这个数是几?

  2019-05-04

• 如果四个两位质数a ，b ，c ，d 两两不同，并且满足，等式 ．那么，(1)a+b 的最小可能值是多少?(2)a+b 的最大可能值是多少?

  2019-05-04

• 桌上放有多于4堆的糖块，每堆数量均不相同，而且都是不大于100的质数，其中任意三堆都可以平均分给三个小朋友，其中任意四堆都可以平均分为四个小朋友，已知其中一堆糖块是17块，则这桌上放的糖块最多是______块。

  2019-05-04

• 把一个两位数质数写在另一个两位数质数右边，得到一个四位数，它能被这两个质数之和的一半整除，那么这样的两个质数乘积最大是（）。

  2019-05-04

• 已知定由"若大于3的三个质数a、b、c满足关系式2a+5b=c，则a+b+c是整数n的倍数"．试问：这个定理中的整数n的最大可能值是多少?请证明你的结论．

  2019-05-04

• 4只同样的瓶子内分别装有一定数量的油。每瓶和其他各瓶分别合称一次，记录千克数如下：8，9，10，11，12，13.已知4只空瓶的重量之和以及油的重量之和均为质数，求最重的两瓶内有多少油？

  2019-05-04

• 自然数N是一个两位数，它是一个质数，而且N的个位数字与十位数字都是质数，这样的自然数有多少个？

  2019-05-04
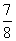• 的分数单位是（    ），它含有（    ）个这样的分数单位，增加（    ）个这样的分数单位是最小的质数。
  2020-05-16
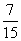• 的分数单位是（     ），再添上（     ）个这样的分数单位就等于最小的质数。
  2020-05-16
• 一个数的百万位上数字是5，万位上数字和百位上数字是10以内最大的质数，个位上数字是最小的奇数，这个数是______，改写成用万作单位的数是______．
  2020-05-16