答:
考虑最差情况:每个抽屉都有1个元素,30÷29=1…1人,剩下的1人,无论怎样分配都会出现一个抽屉有2人出现.1+1=2(人);答:至少有2个学生生日是在同一天.
查看答案
答:
7÷5=1(人)…2(人),1+1=2(人);答:至少有2个人住同一个房间.故答案为:2.
查看答案
答:
b
查看答案
答:
41个
查看答案
答:
c
查看答案
答:
2;2
查看答案
答:
a
查看答案
答:
根据题干分析可得:对于任意的五个正整数a、b、c、d、e除以4最多可以有4个不同的余数0、1、2、3,(1)假设a、b、c、d余数各不相同,那么第五个数e除以4的余数只能是0、1、2、3中的一个余数,这样就和a、b、c、d中的一个余数相同(比如a),那么e-a就是4的倍数.(2).假设a、b、c、d中存在两个数除以3所得余数相同(不妨设是ab),那么a-b就是4的倍数.综上所述,任意5个自然数,至少有两个数的差是4的倍数,这句话是正确的.
查看答案
答:
b
查看答案
答:
正确
查看答案
答:
错误
查看答案
答:
年龄最小6岁,最大13岁,那么一共有13-6+1=8种年龄情况,可以看作是8个抽屉,考虑最差情况:选出8个同学,分别放在8个抽屉中,那么再选出1个同学,无论放到哪个抽屉,都能保证一个抽屉里有2个同学出现,所以8+1=9(个);答:从这个学校中任选9个同学,就一定能保证其中有两位同学的年龄相同.故答案为:9.
查看答案
答:
42张
查看答案
答:
5个,理由“略”
查看答案
答:
“略”
查看答案
答:
4枝
查看答案
答:
b
查看答案
答:
根据抽屉原理的意义可知,“抽屉”至少放的物体的求法是用物体数除以抽屉,当除得的商没有余数时,放的至少数就等于商,当除得的商有余数时,放的至少数就等于商+1.故答案为:抽屉,商,商+1.
查看答案
答:
42张
查看答案
答:
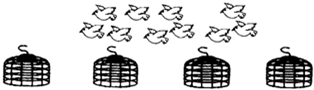
10÷4=2(只)…2(只),2+1=3(只),答:至少有3只鸽子要飞进同一个鸽舍里.故答案为:3.
查看答案