答:
三条线段的长度是连续的整数,如:三条线段的长度是3、4、5能构成三角形;三条线段的长度是1、2、3,2+1=3,不能构成三角形.故答案为:×
查看答案
答:
(1)2厘米+4厘米=6厘米,两边之和等于第三边,不能围成三角形;(2)5厘米+2厘米>5厘米,两边之和大于第三边,能围成三角形;(3)2厘米+2厘米<5厘米,两边之和小于第三边,不能围成三角形.故答案为:×、√、×.
查看答案
答:
因为三角形的内角和是180°,所以:直角三角形中,最大的角是90°,所以另外两个角的度数之和也等于90°,钝角三角形中,最大的角是钝角,大于90°,所以另外两个锐角的度数之和一定小于90°,所以原题说法错误.故答案为:错误.
查看答案
答:
三角形一条边的长度一定大于另外两条边长度的差;故答案为:√.
查看答案
答:
15-8<第三条边<8+15所以7<第三条边<23;故答案为:7,23.
查看答案
答:
cd
查看答案
答:
假设在一个三角形中最多有1个锐角,则另外的两个角都大于或等于90°,于是可得这个三角形的内角和大于180°,这样违背了三角形的内角和定理,假设不成立.所以任何一个三角形的三个内角中至少有两个锐角.故答案为:正确.
查看答案
答:
因为3+3<8,所以等腰三角形的腰的长度是8厘米,底边长3厘米,所以周长是8+8+3=19(厘米)答:围成这个等腰三角形至少需要19厘米长的绳子;故答案为:19.
查看答案
答:
a、3+3>5,符合任意两边之和大于第三边,可以组成三角形;b、4+4>4,符合任意两边之和大于第三边,能围成三角形;c、3+3=6,所以不符合任意两边之和大于第三边,不能围成三角形;故选:b.
查看答案
答:
24÷2=12(厘米),答:最长的一条边的长度要小于12厘米.故答案为:√.
查看答案
答:
c
查看答案
答:
根据三角形的特性:两边之和大于第三边,两边之差小于第三边.且最长边不能超过12厘米的一半.当最长边为5厘米时,其余两边分别为:4厘米、3厘米;当最长边为4厘米时,其余两边分别为:4厘米、4厘米;故答案为:5、4、3、4、4、4.
查看答案
答:
c
查看答案
答:
12-7<第三边<7+12,所以5<第三边<19,第三边的取值在:5厘米~19厘米之间(不包括5厘米和19厘米),所以第三边最小是:6厘米;故答案为:6.
查看答案
答:
d
查看答案
答:
a
查看答案
答:
因为6+4=10,所以三边不能围成三角形;故答案为:×.
查看答案
答:
b
查看答案
答:
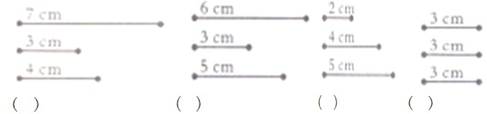
(1)、因为4+3=7,所以不能围成三角形;(2)、因为3+5>6,所以能围成三角形;(3)、因为2+4>5,所以能围成三角形;(4)、因为3+3>3,所以能围成三角形;故答案为:.
查看答案
答:
如果一个三角形中出现2个(或3个)直角或钝角,那么三角形的内角和就大于180°,不符合三角形内角和是180°,所以,三角形中最多有一个钝角或直角,最少有两个锐角;故答案为:1,2.
查看答案