答：
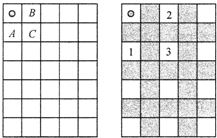
甲先走，按图中阴影的方格走，乙按没有涂色的方格走，答：都按最佳方法走，乙将获胜．
查看答案
答：
先涂色的人只要先占据最中间的一格，创造一个对称状态，此后每次都和对方对称着涂色，当完成最后一次涂色时，对手已无处涂色，于是获胜．
查看答案
答：
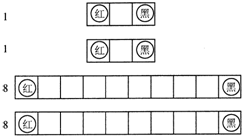
因为操作的数的个数或图形位置能分成完全相同的两份，成对称状态．如果要操作到最后一次为胜，则每次操作后必须是对称状态，这样必胜，即甲走几步，乙相对应的也走几步，这样以来，当甲无路可走时，乙仍然有路走，乙必胜无疑．答：甲走几步，乙相对应的也走几步，这样以来，当甲无路可走时，乙仍然有路走，乙必胜无疑．
查看答案
答：
甲先擦去10，那10的约数2、5、1同时被擦掉，甲再擦的数的个数与乙擦的个数相等，甲将擦完最后一个，甲将获胜．
查看答案
答：
c
查看答案
答：
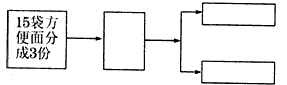
抓阄、转盘、掷筛子等等都可以，因为的这是可能性的问题．首先可以拿出六张纸分别写上1至6号，表示6个班，抽签，抽到几号就是几号上，同样的方法确定同年级谁先上；同样的方法可以换成平均分成几份的转盘来确定，还可以掷筛子来确定，道理是一样的．
查看答案
答：
“略”
查看答案
答：
略,具体答案请查看详情
查看答案
答：
8+7+6+5+4+3+2+1=36（场）
查看答案
答：
7
查看答案
答：
2.5cm
查看答案
答：
c
查看答案
答：
7
查看答案
答：
一个砝码，3克，2克，4克，共3种不同的重量，两个砝码搭配：3克+2克=5克，3克+4克=7克，2克+4克=6克，共3种不同的重量，三个搭配：3克+2克+4克=9克，共有：3+3+1=7（种），答：可以称出7种不同的重量．故答案为：7．
查看答案
答：
略,具体答案请查看详情
查看答案
答：
（1）可以组成的四位数有：2378，2387，2738，2783，2837，2873；3278，3287，3728，3782，3827，3872；7238，7283，7328，7382，7823，7832；8237，8273，8327，8372，8723，8732；共有24个数字；（2）奇数有3和7两个，那么可以构成的单数的可能性就是：2÷4=12；偶数有2和8两个，那么可以构成的双数的可能性就是：2÷4=12．故答案为：24，12，12．
查看答案
答：
c
查看答案
”表示开关，“
”表示电灯，“
”表示电源，电源两端的电线能连成环路灯就会亮，电路中共有l0个开关，每个开关可任选“开”或“关”一种状态，且互相独立．
答：
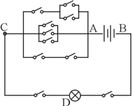
该电路图分为干路和支路，其中支路分为上、中、下三条支路．要想灯亮，则干路为通路，支线至少一条为通路．上支路通路有3种情况，断路则有5种情况；中支路通路有7种情况，断路则有1种情况；下支路通路有1种情况，断路则有3种情况；干路通路只有1种情况：1、上支路通路，中、下支路断路：3×1×3=9种；2、上支路通路，中、下支路通路：3×7×1=21种；3、上支路通路，中支路通路，下支路断路：3×7×3=63种；4、上支路通路，中支路断路，下支路
查看答案
答：
确定百位数字的方法有4种，十位的数字有4种，个位的数字有3种；所以能组成4×4×3=48个不同的三位数．故答案为：48．
查看答案
答：
4分钟
查看答案
