A,B,C,D,E五位选手进行乒乓球循环赛,每两人都只赛一盘。规定胜者得2分,负者不得分。现在知道的比赛结果是:A与B并列第一名(有两个并列第一名,就不再设第二名,下一个名次规定为第三名),D比C的名次高,每个人都至少胜了一盘。试求每人的得分。
【答案】
分析与解:因为乒乓球比赛没有平局,所以求胜的盘数与得分是一回事,胜的盘数乘以2就是得分。五人进行循环赛,共需赛10盘,总得分是2×10= 20(分)。
因为每人都赛4盘,所以第一名最多胜4盘,但因为A,B并列第一,A,B不可能都胜4盘,所以A,B最多各胜3盘。如果A,B没有各胜3盘,而是各胜2盘,那么剩下的10-2×2= 6(盘)的胜利者只会是C,D,E,根据抽屉原理,C,D,E三人中至少有1人胜了至少2盘,与第一名胜2盘矛盾。所以,A,B各胜3盘,各得6分。
还有4盘,已知D比C名次高,每个人都至少胜一盘,只能是D胜2盘得4分,C,E各胜一盘,各得2分。
注意:题目中“每个人都至少胜一盘”是制约结果的重要条件,如果没有这个条件,那么该题的结果就有两种可能:一是A,B各胜3盘,各得6分,D胜2盘得4分,C,E各胜1盘,各得2分;二是A,B各胜3盘,各得6分,D,E各胜2盘各得4分,C胜0盘,得0分。
关注公众号回复:奥数答案
即可免费获得密码查看答案

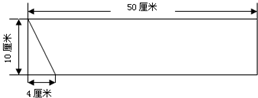
 ,一个长方形少了一块,下面的( )图形补上去,这个长方形就完整了.a.
,一个长方形少了一块,下面的( )图形补上去,这个长方形就完整了.a. b.
b.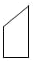 c.
c.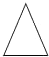
奥数库(www.aoshuku.com)是一个专注奥数知识扩展和学习的在线教育网站,内容涵盖了奥数题、数学题、试卷、课件、知识点、数学公式等,拥有大量的奥数题库和数学题库,包含全国中小学各个版本教材,深受中小学师生用户喜爱的网站。
奥数库专注奥数知识分享,如有版权作品存在问题或内容中存在违法和不良信息,请立即联系403074932@qq.com