六年级奥数题-综合练习题：长方体ABCD-A′B′C′D′中，AB=4，A′A=2′，AD=1，有一只小虫从顶点D′出发，沿长方体表面爬到B点，问这只小虫怎样爬距离最短？（见图（1））-奥数库

题目与解析

问题

六年级奥数题-综合练习题：

长方体ABCD-A′B′C′D′中，AB=4，A′A=2′，AD=1，有一只小虫从顶点D′出发，沿长方体表面爬到B点，问这只小虫怎样爬距离最短？（见图（1））

答案与解析

六年级奥数题-综合练习题：

答案：

　　因为小虫是在长方体的表面上爬行的，所以必需把含D′、B两点的两个相邻的面"展开"在同一平面上，在这个"展开"后的平面上D′B间的最短路线就是连结这两点的直线段，这样，从D′点出发，到B点共有六条路线供选择。

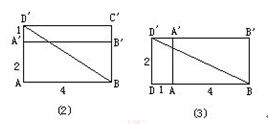
　　①从D′点出发，经过上底面然后进入前侧面到达B点，将这两个面摊开在一个平面上（图（2）），这时在这个平面上D′、B间的最短路线距离就是连接D′、B两点的直线段，它是直角三角形ABD′的斜边，根据勾股定理，

　　D′B2=D′A2+AB2=（1+2）2＋42=25，

　　∴D′B=5

　　②容易知道，从D′出发经过后侧面再进入下底面到达B点的最短距离也是5

　　③从D′点出发，经过左侧面，然后进入前侧面到达B点。将这两个面摊开在同一平面上，同理求得在这个平面上D′、B两点间的最短路线（图（3）），有：

　　D′B2＝22+（1+4）2=29。

　　④容易知道，从D′出发经过后侧面再进入右侧面到达B点的最短距离的平方也是29。

　　⑤从D′点出发，经过左侧面，然后进入下底面到达B点，将这两个平面摊开在同一平面上，同理可求得在这个平面上D′、B两点间的最短路线（见图），

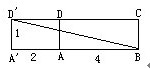
　　D′B2=（2+4）2+12=37。

　　⑥容易知道，从D′出发经过上侧面再进入右侧面到达B点的最短距离的平方也是37。

　　比较六条路线，显然情形①、②中的路线最短，所以小虫从D′点出发，经过上底面然后进入前侧面到达B点（图（2）），或者经过后侧面然后进入下底面到达B点的路线是最短路线，它的长度是5个单位长度。

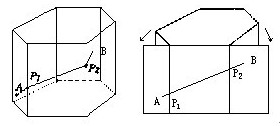
　　利用前面的题中求相邻两个平面上两点间最短距离的旋转、翻折的方法，可以解决一些类似的问题，例如求六棱柱两个不相邻的侧面上A和B两点之间的最短路线问题（下左图），同样可以把A、B两点所在平面及与这两个平面都相邻的平面展开成同一个平面（下右图），连接A、B成线段AP1P2B，P1、P2是线段AB与两条侧棱线的交点，则折线AP1P2B就是AB间的最短路线。