（1）三角形向右平移3格后的图形．
（2）三角形绕点o按逆时针方向旋转90°后的图形．
（3）三角形按2：1放大后的图形．
答：
根据题干分析可以画图如下：
查看答案
答：
13×3.14×42×6，=13×3.14×16×6，=100.48（立方分米）；答：得到的立体图形是圆锥体．它的体积是100.48立方分米．
查看答案
答：
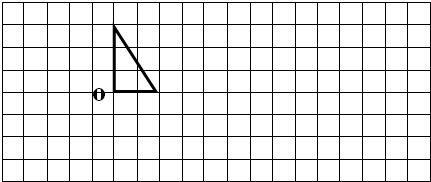
（1）先把旗杆绕点o逆时针旋转90°，再根据三角旗的特点画出旗面，即可得出旋转后的图形1；（2）先把三角旗的各个顶点向下平移2个，再依次连接起来即可得出平移后的图形2，如图所示；
查看答案
b．
c．
d．
答：
b
查看答案
画出图①的另一半，使它成为一个轴对称图形．再将画好的完整图形先向右平移6格．
答：
（1）根据轴对称图形的性质画出图形①的另一半如图所示，再利用图形平移的方法，将这个图形的各个顶点向右平移6格，再依次连接起来即可得出平移后的图形；（2）图中圆的圆心的位置用数对表示是（3，3），o点的位置可用数对表示是（11，3）．将圆按3：1的比放大，并以o点为圆心画出放大后的圆，如图所示：则原来圆的面积和放大后圆面积的比是（1：9）．（3）先把与点a相连的两条边顺时针旋转90，即可画出旋转后的图形，如图所示：
查看答案
答：
作图如下图：
查看答案
答：
2×3.14×2×5=62.8（平方厘米）3.14×22×5=3.14×4×5=31.4（立方厘米）答：它的侧面积是62.8平方厘米；体积都是31.4立方厘米．
查看答案
答：
令直角三角形的直角边分别为3、4，斜边为5；（1）绕它较短的一条直角边旋转一周得到圆锥的体积为：13×3.14×42×3，=13×3.14×16×3，=50.24，答：体积为50.24．（2）绕直角边4旋转一周得到圆锥的体积为：13×3.14×32×4，=13×3.14×9×4，=37.68，答：体积为37.68．（3）绕斜边5旋转一周，得到的是一个不规则的立体图
查看答案
答：
（1）抓住以a为顶点的两条边，将其顺时针旋转90°，再根据长方形的性质即可画出这个长方形1，选择后的图形有2条对称轴，如图所示；（2）根据图形放大与缩小的性质，将三角形按1：2的比缩小后得到三角形2，如图所示，缩小后的三角形与原三角形相似，相似比为1：2，则面积之比等于相似比的平方为1：4，即缩小后三角形的面积是原来的25%；故答案为：（1）2；（2）25．
查看答案
答：
根据题干分析作图如下：
查看答案
答：
如图：把图形a向右平移4格可以得到图形b；图形b绕点0，顺时针方向旋转90°得到图形c．故答案为：右，4，顺，90°．
查看答案
答：
3.14×42=3.14×16=50.24（平方厘米）答：将一个直角三角形绕它较短的一条直角边为轴旋转一周后所得的图形是圆锥体，它的底面积是50.24平方厘米．故答案为：圆锥体，50.24．
查看答案
答：
（1）3.14×22×4+13×3.14×22×3，=50.24+12.56，=62.8（立方厘米），（2）3.14×22×（3+4）-13×3.14×22×3，=87.92-12.56，=75.36（立方厘米），答：这个组合图形的体积是62.8立方厘米或者75.36立方厘米．
查看答案
答：
把下面的图形以直线为轴旋转一周，在能形成圆柱的图形下面画“√”．
查看答案
答：
以6cm为轴旋转得到的圆柱的侧面积：2×3.14×2×6=75.36（cm2），体积：3.14×22×6=3.14×4×6=75.36（cm3）；以2cm为轴旋转得到的圆柱的侧面积：2×3.14×6×2=75.36（cm2），体积：3.14×62×2=3.14×36×2=226.08（cm3）；75.36cm2=75.36cm2，75.36
查看答案
答：
3.14×102×3=3.14×100×3=942（立方厘米）答：得到的圆柱体的体积是942立方厘米．
查看答案
答：
13×3.14×42×3=13×3.14×16×3，=50.24（cm3）；答：以短边为轴旋转一周得到一个圆锥体；这个圆锥体的体积是50.24cm3．
查看答案
答：
3.14×52×2，=3.14×25×2，=78.5×2，=157（立方厘米）；答：这个圆柱体的体积最大是157立方厘米．
查看答案
答：
3.14×52×8=3.14×25×8=628（立方厘米）；答：得出的立体图形的体积是624立方厘米．故答案为：628．
查看答案
答：
以4厘米为旋转轴形成的立体图形体积：13×3.14×（6÷2）2×（4÷2）×2=13×3.14×9×2×2，=37.68（立方厘米），以6厘米为旋转轴形成的立体图形体积：13×3.14×（4÷2）2×（6÷2）×2=13×3.14×4×3×2，=25.12（立
查看答案
