路程的计算问题大全及答案
更新时间:2021-06-23
类型:小学六年级数学题
题数:359
答:
(1)180:3;60:1(2)150:2.5;60;速度(3)速度;路程;时间;正(4)60;1.2;180:3;比例;3;外项;180;内项;3;180
查看答案
答:
速度和时间是两种相关联的量,它们与路程有下面的关系:速度×时间=路程(一定);已知路程一定,也就是速度与时间的乘积一定,所以速度与时间成反比例.故答案为:反
查看答案
答:
因为车轮所行路程:转数=车轮的周长=车轮的直径×π(一定),是对应的比值一定,所以车轮所行路程和转数成正比例关系;故答案为:正.
查看答案
答:
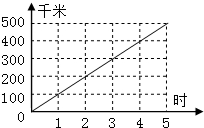
1.路程和时间的比,也就是速度,其值为100是定值,所以路程和时间成正比例2.2.5×100=250(千米);520÷100=5.2(小时)
查看答案
答:
(1)根据图可知:路程÷时间=速度(一定),所以路程和时间成正比例关系;(2)100÷1×5.5=550(千米);故答案为:正,550.
查看答案
答:
所走路程和剩下路程虽然是两种相关联的量,但是所走路程与剩下路程相加是总路程,它们是加数、加数与和的关系.它们的比值和乘积都不是一定的,所以已行的路程和剩下的路程不成任何比例关系.故答案为:不成比例.
查看答案
答:
圆柱的体积一定,底面积和高成反比例;速度一定,路程和时间成正比例;故答案为:反、正.
查看答案
答:
3.6千米=3600米,1小时=60分,小勇走的路程和时间的比:120:2=60:1,小健走的路程和时间的比:3600:60=60:1;因为120:2=60:1=60÷1=60,3600:60=60:1=60÷1=60,两个比的比值相等,所以他们俩各自走的路程和时间的比能组成比例.答:小健说得对.
查看答案
答:
行驶的路程:速度=时间(一定),是对应的比值一定,所以行驶的路程和速度成正比例;故答案为:正.
查看答案
答:
260÷(320÷80×10%)=650(千米)
查看答案
答:
18÷(1-35%)≈27.7(千米)
查看答案
答:
(19-110)÷19,=190÷19,=10%;答:甲每分钟行的路程比乙每分钟行的路程少10%;故答案为:10.
查看答案
答:
4.8÷40%-4.8=7.2(小时)
查看答案
答:
0.6×3.14×100=188.4(米)1884÷188.4=10(分钟)答:需要骑10分钟。
查看答案
答:
3.14×82÷2=100.48(平方厘米);2×3.14×10×24=1507.2(厘米)
查看答案
答:
根据分析可得,甲的速度是乙的3倍,把乙的路程看成1份,则相同时间内甲的路程为3份,整个跑道为4份,乙从第一次相遇到第二次相遇,正好走了一个1份,所以这个100米就是乙的路程,环形跑道的长度为:100×4=400(米);答:环形跑道有400米.
查看答案
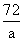 =( ),a=( )。y:x=( ):( ),这个式子叫做( ),y和( )叫做比例的( ),x和( )叫做比例的( ),且有y·( ) =x·( )。
=( ),a=( )。y:x=( ):( ),这个式子叫做( ),y和( )叫做比例的( ),x和( )叫做比例的( ),且有y·( ) =x·( )。