题目与解析

答案与解析

首先研究能被9整除的数的特点：如果各个数位上的数字之和能被9整除，那么这个数也能被9整除;如果各个位数字之和不能被9整除，那么得的余数就是这个数除以9得的余数。

解题：首先，任意连续9个自然数之和能被9整除，也就是说，一直写到2007能被9整除。所以答案为1

关注公众号回复：奥数答案

即可免费获得密码查看答案

密码错误

查看答案

微信搜索天才奥数关注公众号

手机扫码关注公众号

查看答案

查看答案

密码错误

热题推荐

• 下图中已经画出了三个图，请将第四个图补全，并按规律画出第22个和第29个图。

  

  2020-05-16
• 一年级某班42名同学围成一圈做游戏，由班长起从1开始按顺序报数，谁报到100就给同学们讲一个故事，然后再由这名同学开始报数．那么第一个讲故事的同学与第二个讲故事的同学中间隔着（    ）个同学。
  2020-05-16
• 根据下面的式子，请计算后面的两道题。
  1+3=4-2×2，1+3+5=9=3×3，1+3+5+7=16=4×4，
  1+3+5+7+9=□=□×□
  1+3+5+7+9+11+13+15+17=□=×□
  2020-05-16
• 三种珠子依次排列如图●●○○○◎◎●●○○○◎◎……第33个珠子是

  [     ]

  a．●
  b．○
  c．◎
  2020-05-16
• 用小棒搭房子，搭三间用了13根，如右图，照这样搭502间房子要用

  

  [     ]

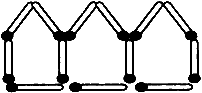
  a．2007根  
  b．2008根
  c．2009根
  2020-05-16
• 找规律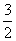、、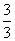0.75、60%、（   ）（填小数）、（   ）（填分数）。
  2020-05-16
• 按规律填数：1，-3，5，-7，（　　）a．9，-11b．9，11c．-9，11
  2020-05-16
• 将1、1、2、2、3、3、4、4这八个数字排成一个八位数，使得两个1之间有一个数字，两个2之间有两个数字，两个3之间有三个数字，两个4之间有四个数字，那么这样的八位数中的一个是几？
  2020-05-16
• 观察下列等式：
  11×2=1-12；12×3=12-13；13×4=13-14；1n×(n+1)=1n-1n+1；…
  将以上n个等式相加得11×2+12×3+13×4+…+1n(n+1)=1-1n+1
  利用上述结论计算：11×2+12×3+13×4+…+199×100
  其结果是______．
  2020-05-16
• 观察并完成序列：b，1，f，f，1b，______，21，28．
  2020-05-16