答:
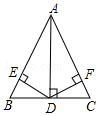
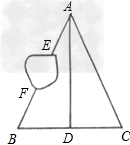
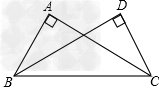
∠bad=∠cad或∠adb=∠adc.
查看答案
答:
4
查看答案
答:
hl
查看答案
答:
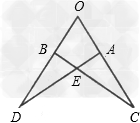
△aed≌△aec,△abd≌△abc,△ebd≌△ebc
查看答案
答:
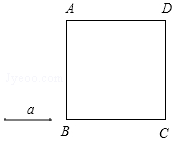
解:(1)作图如下:(2)图中的四个直角三角形全等:rt△aeh≌rt△bfe≌rt△cgf≌rt△dhg.证明rt△aeh≌rt△bfe,理由如下:∵abcd是正方形,∴ad=ab,∠a=∠b=90°,∵ae=bf=cg=dh,∴ah=be,∴rt△aeh≌rt△bfe(sas).
查看答案
答:
12
查看答案
答:
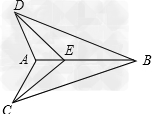
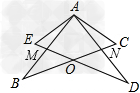
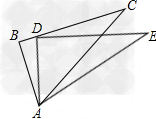
解:(1)∵∠dac=∠bae,∴∠bac=∠dae,又∵ab=ad,ac=ae,∴△bac≌△dae,∴bc=de;(2)∵由(1)得,∠b=∠d,∠ban=∠dam,ab=ad,∴△adm≌△abn,∴am=an,bn=dm。
查看答案
答:
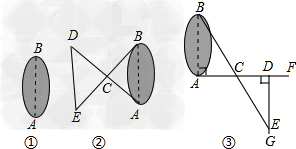
解:设计一,如图1,(1)过a作线段ad⊥ab;(2)过d作dm⊥ad;(3)取ad中点c,连接bc并延长交dm于e,则de长就是隧道ab的长,理由:因为ad⊥ab,ed⊥ad,所以∠a=∠d=90°,又∵ac=cd,∠acb=∠dce,所以△abc≌△dec,所以ab=de,设计二,如图2,(1)过a作线段ad;(2)取ad中点c,连接bc并延长,使ec=bc;(3)连接de,则de就是隧道ab的长,理由:因为ac=dc,&
查看答案
答:
c
查看答案
答:
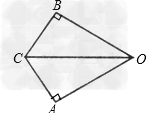
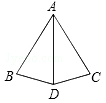
解:由题意,知bd=cd,∠bda=∠cda=90°,ad=ad,则△adb≌△adc,所以ab=ac=3,故斜拉桥至少有3﹣1.2﹣0.7=1.1(千米)。
查看答案
答:
b
查看答案
答:
8
查看答案
答:
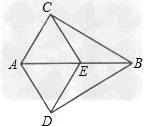
证明:(1)∵ab=ab,∠acb=∠adb=90°,ac=ad,∴rt△acb≌rt△adb,∴∠cba=∠dba,即点a在∠cbd的平分线上;(2)ce=de,理由:由(1)知,∠cab=∠dab,∵ac=ac,ae=ae,∴△ace≌△ade,∴ce=de。
查看答案
答:
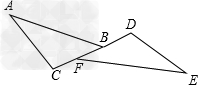
解:图②的设计方案:(1)先在岸上取一点c,从该点可以直达a点和b点;(2)连接ac并延长到点d,使cd=ac;(3)连接bc并延长到点e,使ce=bc;(4)连接de,并测出它的长度.de的长度就是a,b两点间的距离,理由:在△abc和△dec中,因为cb=ce,∠acb=∠dce,ac=cd,所以△abc≌△dec,则ab=de;图③的设计方案:(1)在ab的垂线af上取两点c,d,使cd=ac;(2)过点d作af的垂线dg,并在dg上取一点e,使点b,c,e在同一条直线上;(3)测得
查看答案
答:
a
查看答案
答:
120°
查看答案
答:
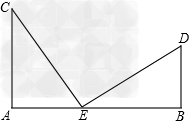
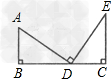
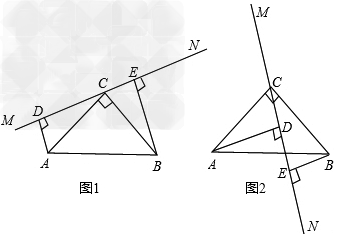
解:(1)理由:因为∠acd+∠acb+∠bce=180°,∠acb=90°,所以∠acd+∠bce=90°.又ad⊥mn,be⊥mn,则∠adc=∠ceb=90°,∠dac+∠acd=90°故∠dac=∠ecb而ac=cb所以△adc≌△ceb(aas);(2)等量关系:de=ad+eb,理由:由(1)知△adc≌△ceb,则ad=ce,dc=eb,
查看答案
答:
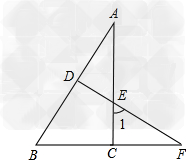
解:(1)∠1=∠b理由:由∠acb=90°,知∠1+∠f=90°又df⊥ab,所以∠b+∠f=90°则∠1=∠b;(2)ab=fb理由:在△abc和△fbd中,∵∠acb=∠fdb=90°,bc=bd,∠b=∠b,∴△abc≌△fbd,∴ab=fb。
查看答案
答:
b
查看答案
答:
c
查看答案